Part IV: Color Temperature

One the most abused and misunderstood terms in reef aquarium lighting is color temperature. Lamps, both fluorescent and metal halide, are being sold in the hobby based on color temperature ratings ranging from 5000K to 50000K, with a wide range of values in between. It is not uncommon to find lamps rated as 6500K, 10000K, 11000K, 12000K, 12500K, 13000K, 14000K, 15000K, 18000K, 20000K and 50000K being sold in the hobby. As interpreted by reef aquarists, these numbers tend to convey the apparent "blueness" of the light emitted by the lamps. The aquarium lighting industry has used this color temperature interpretation as a way to label their lamps, and use it to signify how their lamps would appear in comparison to other lamps and as a selling point for their lamps. It has been my experience, however, that these numbers often seem to be rather arbitrarily created and often there is very little correlation between the scientifically defined term of color temperature and the label on the lamp, thereby making it more difficult for the aquarist to make choices based on color temperature ratings. In this article I will explain the concept of color temperature, its relationship to spectral power distribution, and the color temperature nuances of light sources.

Understanding color temperature starts with understanding black body radiation and the Kelvin temperature scale. A theoretical black body is an object that has no color and is "black" because it absorbs all radiation incident on its surface and emits no radiation at 0° Kelvin. In the Kelvin temperature scale, 0° Kelvin (abbreviated by K) corresponds to -273.16° C and is the temperature where all molecular motion has ceased. This is called absolute zero. Recall that for radiation to be generated, the electrons have to be jumping to higher energy levels and releasing the energy as photons. At absolute zero all motion ceases and there is no energy being emitted. Hence, at 0K the black body emits no radiation.

As the black body is heated above 0°K it starts to emit radiation that lies within the electromagnetic spectrum. The radiation's spectral distribution depends on the black body's temperature. At low temperatures (e.g. room temperature) the black body is emitting radiation, but it is not in the range that is part of the visible spectrum. For visible radiation the back body must be quite hot. At about 1000K it looks red, yellow at about 1500K, white at 5500K, bluish-white at 6500K and more bluish at 10000K. The spectral irradiance of the radiation and color changes with temperatures have been well studied by physicists, and the relationships are given by the well-known black body radiation laws. Plank's law gives the spectral irradiance at different wavelengths, Wien's law provides the wavelength at which the peak irradiance occurs, and Stephan Boltzman's law relates the total amount of energy to the temperature of the black body. Details of these can be found in any physics textbook and will not be covered here.

Figures 1-3 below show the radiation of the black body at different temperatures and the peak of the radiation. It also shows the visible portion of the radiation as colored bands. This is how a perfect black body radiator behaves, and the radiation is a function of the temperature to which it is heated.

How does this relate to the light sources we use - fluorescent and metal halide lamps? Does this mean that a lamp being sold as a color temperature of 20000K is a black body radiator and has an actual physical temperature of 20000K? No, since the lamps are not black body radiators! To be able to assign a color temperature to a light source there must be a color match as well as a spectral match to a black body radiator. The spectral output of fluorescent lamps and metal halide lamps does not match with the black body spectral irradiance. Hence, the term color temperature, in fact, does not apply directly to these light sources. What it really means is that if we were to compare the lamp's color to a black body at 20000K, it would appear the same to a human observer. The technically correct term for this is Correlated Color Temperature (CCT) which is defined as the value of the temperature of the black body radiator when the radiator color matches that of the light source. CCT implies a color match to a black body at the specified temperature, but there is no spectral match. The table below shows CCT of various light sources:

This now brings up the issues of matching lamp color to color temperatures of the black body. Once we start talking about color, we have to remember that color is not a physical property but a physiological response created in the brain by the visible light seen by the eye. As someone adequately surmised, "Color is only a pigment of your imagination."

To be able to work with color mathematically, scientists have developed a mathematical means to specify color - where color is specified by numerical values called color coordinates or chromaticity. Correlated Color Temperature (CCT) can be determined by mathematical formula to find the chromaticity coordinates of the black body's color temperatures that are closest to the light source's chromaticity. (More on chromaticity and how it developed later.)

Since it is a single number, CCT is simpler to communicate than chromaticity or SPD, and is used as a shorthand for reporting the color appearance of light emitted from electric light sources. Correlated Color Temperature values are being used by the reef lighting industry to give a general indication of the apparent "blueness" of the light emitted by the source. According to aquarium lighting industry convention, lamps with higher CCT values provide light that appears "more blue."

To develop a mathematical and more unambiguous definition of color and color perception, the International Lighting Commission (Commission Internationale de l'Eclariage, referred to as CIE) established a colorimetry system for color matching that has, with minor changes, remained in use for the last 75 years. To understand the proper definition and meaning of CCT we need to understand color vision, how the chromaticity diagram was established, and how it is used to determine CCT of light sources.

Color Vision

Before understanding the CIE color diagram, it is important to understand how the human eye sees color. The human eye contains two different kinds of receptors - rods and cones. The rods are more sensitive and outnumber the cones, but the rods are not sensitive to color. Color vision is provided by the cones. There are basically three types of color sensitive cones in the human eye, corresponding roughly to red, green and blue. The response curves of these different cones have been mapped by researchers. The perception of color depends on the neural response of the three types of cones. Hence, it follows that visible color can be mapped in terms of the response functions of these three types of cones. It was shown that color samples could be matched by combinations of monochromatic colors: red (700 nm), green (546.1 nm) and blue (435.8 nm). These matching functions were determined by experiments. By simply adding various amounts of these primary colors a large range of colors could be matched, but there were still some outside this range that could not be matched by pure addition. It was found, however, that by allowing negative values of red, all colors could be matched. Allowing negative values of red is the same as adding red to the color sample being matched.

CIE Chromaticity Diagram

The CIE matching functions were derived from these Red, Green and Blue matching functions such that the matching functions are all positive, and any color can be considered to be a mixture of the three CIE primaries. These "primary colors" can be represented as mathematical functions of their wavelength, and are shown in Figure 4 below. The most commonly used CIE primaries were developed in 1931 using a two-degree field of view; since then, others have been defined using a 10-degree field of view and the functions were updated in 1964.

The CIE color coordinates are derived by weighting the spectral power distribution (obtained by using a spectroradiometer) by these three functions. This gives three values, called the tristimulus values (X, Y, Z), from which the chromaticity coordinates are calculated. Without going into the mathematics of computing these values (we can let a program compute them), the Y value is a measure of luminosity, or how bright the light appears to an observer. These Y values are, in fact, defined to be the same as the photopic response of the human eye. Because perceived color depends on the relative magnitudes of X, Y and Z, the chromaticity coordinates are usually given by normalized coordinates x and y, where x = X/(X+Y+Z), y = Y/(X+Y+Z) and x+y+z = 1. The (x, y) coordinates are called the chromaticity coordinates. In the computation of the chromaticity coordinates the Y value is normalized to 100.

The figure below shows the 1931 CIE chromaticity diagram. The color temperature of a true black body is also shown on this chart. The path taken by the black body color temperature is called the black body locus. The pure spectrum colors appear on the outside along the curve, and points representing non-spectral colors are inside. A straight line connects the ends and represents colors that are combinations of wavelengths of 400 nm and 700 nm (blue and red).

Mathematically, the Correlated Color Temperature of a light source is computed by determining the (x,y) color coordinates of the light source, and by finding the color temperature closest to the lamp (x,y) that lies on this black body locus. Details of this approach are beyond the scope of this article, but interested readers are referred to Reference 1.

What is important to note is that using such an approach, two points on either side of the black body locus can have the same CCT but different color coordinates. To prevent this from creating large differences in the perceived color of light represented by the same color temperature, a small tolerance zone is typically specified near the black body locus, and if the two points are outside this tolerance, then larger color differences will be perceived.

One drawback of the 1931 chromaticity diagram is the fact that equal distances on the chart do not represent equally perceived color differences because of the non linear nature of the human eye. The 1976 uniform chromaticity CIE chart (Figure 6) was developed to provide a perceptually more uniform color spacing for colors at approximately the same luminance. The coordinates used here are denoted (u',v') and can be computed from the 1931 x,y coordinates by the following transformation:

u'= 4x / (-2x + 12y + 3)

v'= 9y / (-2x + 12y + 3)

This excellent website provides the mathematical equations and a calculator to convert between the various color coordinates developed. In spite of its drawbacks, the 1931 color chart is still one of the most popular in use.

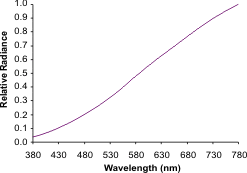
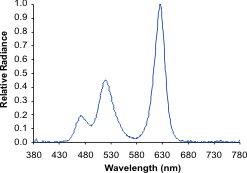
Another artifact of using the CCT arises from the fact that a single number is once again being used to characterize the SPD of the lamp. It is very possible that two very different spectral power density functions can have the same CCT, as shown in the Figure 7 below taken from http://www.lrc.rpi.edu/.../lightsources/measure.asp. Light sources with different spectral distributions but with the same CCT are called metameric light sources.

Spectral power distribution of two metameric light sources:

While it is too complex to represent the color appearance of a light source precisely by the color coordinates, it does provide a useful approximate representation of the appearance of the light source. The color theory can mathematically represent color and provide a mathematical specification of color, yet there is still a difference between color specification and humans' color experience. For example, brown and orange can have the same color coordinates on a CIE chart, but both produce a very different color experience in the human eyes. This artifact of color appearance is very difficult to represent in the CIE color chart and its mathematical representation of color. This situation arises due to the normalization of the luminosity function.

Color Coordinates of Metal Halide Lamps

As seen from the above discussion, the main input required to calculate the CIE chromaticity coordinates is the spectral distribution and the functions for the CIE primary colors. The spectral data is obtained using the Licor 1800 Spectroradiometer. Software for the spectroradiometer has built-in functions to compute the 1931 CIE color coordinates. Using this, the color coordinates of a sampling of "blue" 250-watt mogul metal halide lamps sold as 13000K, 14000K and 20000K are computed and shown in the table below.

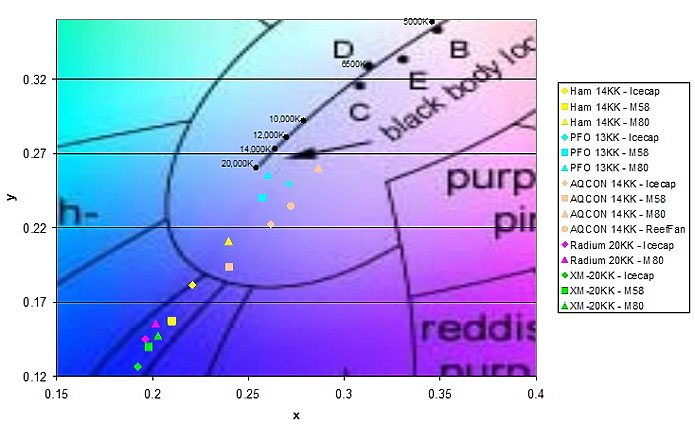
These chromaticity coordinates are plotted on the CIE diagram, as shown in Figure 8 below. The background color for the plot is obtained by superimposing the color diagram from Figure 1. The plot is scaled to show only the relevant piece of the chart.

CIE (1931 2deg) Chromaticity Coordinates of 250-watt Mogul "Blue" Lamps:

Summary

This article presented an overview of how color temperature is correctly defined and what it means. For lamps used in the aquarium hobby - both fluorescent and metal halide - the correct term to describe the color temperature is the Correlated Color Temperature (CCT). Correlated color temperature is derived from the chromaticity coordinates of the lamp, which, in turn, are determined by the spectral power distribution and the CIE color matching functions. Based on the mathematically accepted definitions, we should expect the CCT of metal halide lamps sold in the hobby to be close to black body locus, in the vicinity of their specified color temperature. Unfortunately, this is not the case with most metal halide lamps, especially the ones that have significantly "blue" appearance.

References

A. R. Robertson, "Computation of Correlated Color Temperature and Distribution Temperature," J. Opt. Soc. Am. 58, 1528- (1968).